The arrow of time

by Eric Holmberg

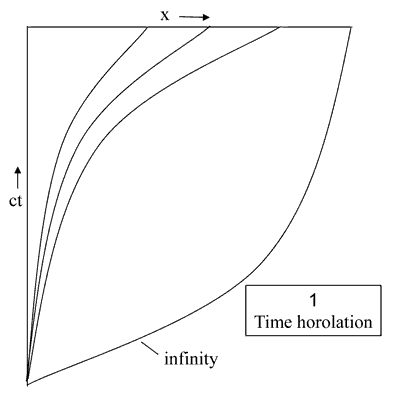
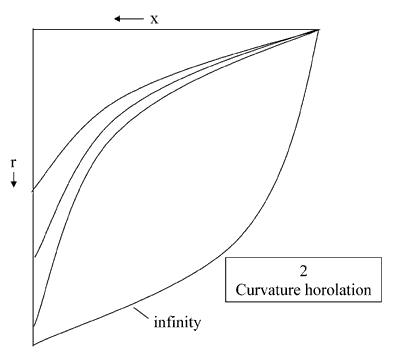
Since the "world without time" paper was posted the author has come to feel that the model it describes could be improved in one or two places and that it actually omits one important consequence. The present paper is intended to rectify these defects.

Dealing first with the omission: it is that the problem of the arrow of time is solved by the fact that time and the curvature factor share an axis so that both are parabolic not hyperbolic. Thus what would be the negative part of the time axis does not exist. Its place is taken by the curvature variable.

Returning to the paper generally, it does not make it clear that dilation occurs in both the time and position aspects of the geometry. If this were not so, the velocity of light would not remain constant. This argument is however an appeal to physical knowledge. What we need is a geometric reason to back it up. The geometries of the time and of the curvature aspects are not in question; what we lack is a clear link between them.

This link is a structure known as a horo-sphere, a sphere with its centre at infinity, We can see where this fits in if we analyse the process of moving the origin a distance x, say. It should be borne in mind that the picture of space produced is the one experienced by an observer located at the origin. To keep matters simple we shall consider the case of a single space or position line.

It will make matters clearer if we divide the process into two stages, first setting the scene as it were then tracing the actual movement.

In Reference 3 it was pointed that the difficulties encountered in Reference 2 are removed if one accepts that the extra dimension of space is duplex and that time in one part is replaced by a variable representing curvature in the other. The two extra component parts are not hyperbolic like the main body but parabolic; the extra dimension is split into two. Parabolic spaces are not familiar objects in geometry but in this case it is clear that they can be characterised by a co-ordinate framework consisting of a horo-lation. See Reference 1 page 83. In one the horo-lation is centred about the time axis, in the other about the position line. See Figures 1 and 2.

The horo-lation in the time space can be used as in Reference 2 to define the velocity of the origin:
v/c = tanh x = cos A (Figure 1)

The horo-lation in the curvature space defines the universal curvature:
r/w = sech r = sin B (Figure 2)
where w is the proper measure of distance corresponding to s, the proper time, and r is the radius of curvature. See Figure 2.

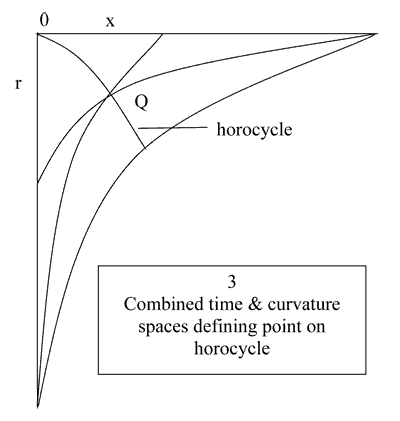
The crux of this analysis is that both the position and the radius of curvature lines are part of the furniture as it were so a length on the curvature line is numerically the same as an equal distance on the position line. Similarly the two angles A and B are equal. If now the two parabolic spaces are put together the expressions, for velocity and curvature, in the form cos A and sin A represent the parametric co-ordinates of a circle. If circular is replaced by linear measure as in the parallel angle formula the circle becomes a horo-cycle with the coordinates of a general point Q tanh x and sech x. See Figure 3.

The scenario for a change in the position of the origin is then as follows: first the radius of curvature or scale factor makes a jump from one to sech(x'/R) causing the point Q to move away from the origin; the movement of Q also signals a boost in the velocity of the origin from zero to tanh(x/R). From then on Q moves back along the horo-sphere to its starting point. As Q moves so does the origin at a velocity determined by the parallel angle formula. One cannot infer a duration in time for this movement because the approach to rest at the destination is asymptotic; the velocity at every point is equal to the remaining distance to be travelled.
When the jump of the scale factor occurs a virtual image of the time axis moves a distance x along the position axis to its eventual destination. This is because the origin has not moved at this stage although its velocity has been booted. In order to experience the change of curvature an observer has to be on a dilated line, so when the time axis moves away a (dilated) hyper-cycle is created passing through its original position. The movement of the
origin is then accomplished by drawing the hyper-cycle up to its formerly virtual position. Again, for the benefit of non-geometers, a hyper-cycle is what would be called in Euclidean geometry a parallel line; however, unlike in Euclidean geometry, it is now dilated by a factor equal to the cosh of the distance between it and its parallel.

While the movement of the origin is proceeding the return of Q to its starting point means that the radius of curvature also returns to its initial value of unity. Thus although the position of the origin has changed the value of the radius of curvature has not; there has been no permanent expansion of position space.

It will be noted, and seen in Figure 3, that there comes a point at which the radii for curvature and velocity coalesce into a single line touching at either end the position and curvature axes. The co-ordinates of Q are then (1 , 0) representing maxima for velocity and scale factor. This, clearly, is the depiction of a light ray. The velocity called for is its maximum but it is finite; its destination however is infinitely distant. It is therefore constrained to run on indefinitely or until it is obstructed. The model set out above therefore accurately describes the behaviour of light.

References

1. Hyperbolic Geometry. Birger Iversen. LMS
Student texts 25. 1992.
Proceedings of the biennial conference devoted to the "Physical interpretation of relativity theory" – PIRT
2. PIRT VIII pp 196-202 September 2002
3. PIRT XI pp 274-288 September 2004

Back to the top

<<PREVIOUS